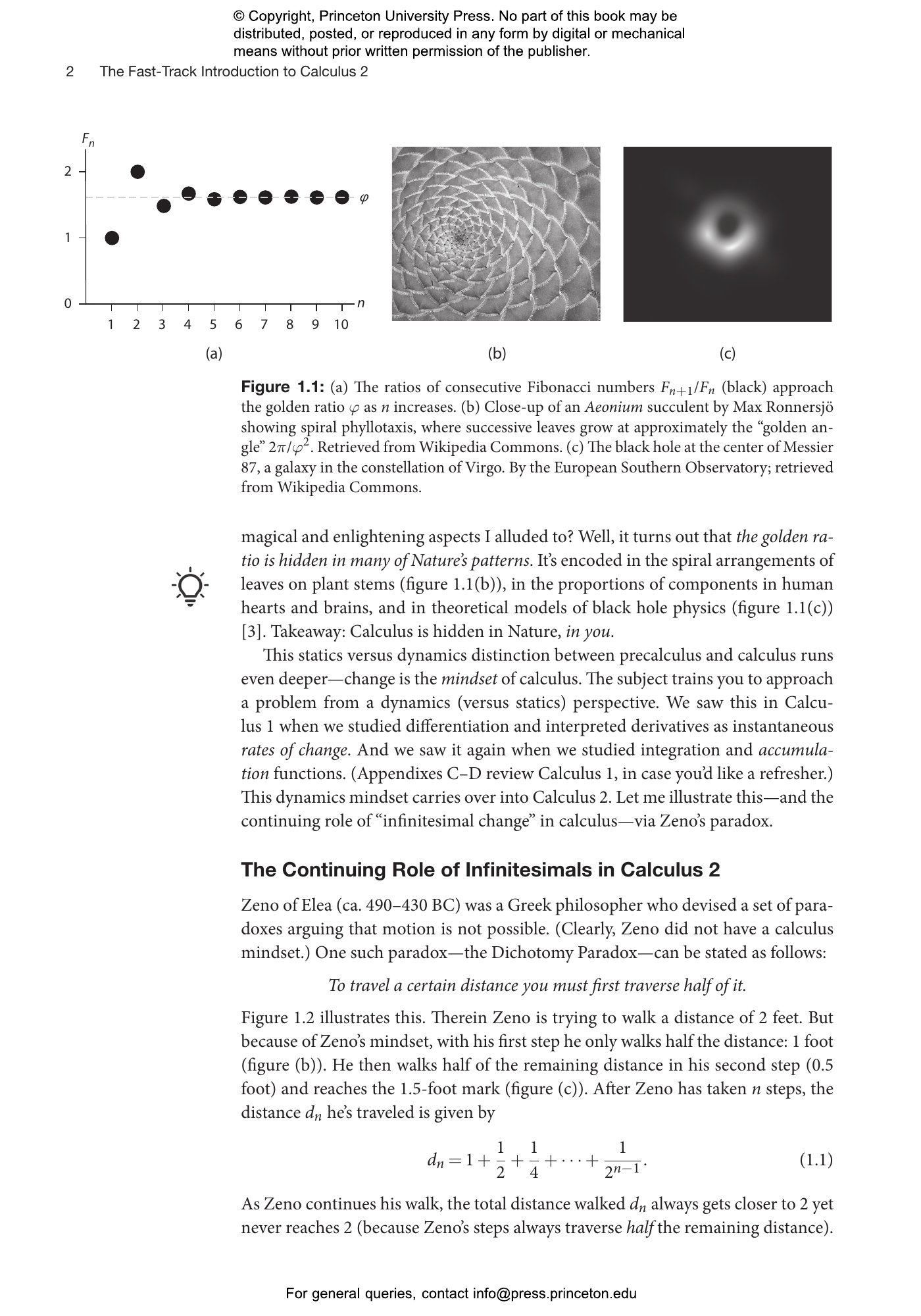
Second-semester calculus is rich with insights into the nature of infinity and the very foundations of geometry, but students can become overwhelmed as they struggle to synthesize the range of material covered in class. Oscar Fernandez provides a âGoldilocks approachâ to learning the mathematics of integration, infinite sequences and series, and their applicationsâthe right depth of insights, the right level of detail, and the freedom to customize your student experience. Learning calculus should be an empowering voyage, not a daunting task. Calculus 2 Simplified gives you the flexibility to choose your calculus adventure, and the right support to help you master the subject.
- Provides an accessible, user-friendly introduction to second-semester college calculus
- The unique customizable approach enables students to begin first with integration (traditional) or with sequences and series (easier)
- Chapters are organized into mini lessons that focus first on developing the intuition behind calculus, then on conceptual and computational mastery
- Features more than 170 solved examples that guide learning and more than 400 exercises, with answers, that help assess understanding
- Includes optional chapter appendixes
- Comes with supporting materials online, including video tutorials and interactive graphs
Oscar E. Fernandez is professor of mathematics at Wellesley College. He is the author of Calculus Simplified; The Calculus of Happiness: How a Mathematical Approach to Life Adds Up to Health, Wealth, and Love; and Everyday Calculus: Discovering the Hidden Math All around Us (all 91ÌÒÉ«).
- Preface
- Before You Begin
- To the Student
- To the Instructor
- 1 The Fast-Track Introduction to Calculus 2
1.1 First Things First: What Is Calculus?1.2 Limits: (Still) The Foundation of Calculus1.3 The Three Diï¬cult Questions That Drove the Development of Calculus 2
- 2 Integration Techniques and Approximations
2.1 Integrating, Leibnizâs Way2.2 Approximating Integrals, Riemannâs Way2.3 The Trapezoidal Rule2.4 How to Approximate Integrals to Any Desired Accuracy2.5 Integration by Parts2.6 Trigonometric Integrals2.7 Trigonometric Substitution2.8 Partial Fraction Decomposition2.9 Parting ThoughtsChapter 2 AppendixA2.1 Evaluating Riemann Sums Using Summation FormulasA2.2 Additional Error Theorems for Riemann Sums and the Trapezoidal RuleA2.3 The Tabular Method for Integration by PartsA2.4 Integrands That Are Products of Powers of Sine and CosineA2.5 Integrands That Are Sine-Cosine Products with Diï¬erent ArgumentsA2.6 A Brief Review of Long Division and Its Uses in Partial Fraction Decomposition
- 3 Applications of Integration
3.1 A Quick Preview of Whatâs to Come3.2 Area between Curves3.3 Volumes by Cross Sections3.4 Volumes of Revolution: The Disk Method3.5 Volumes of Revolution: The Washer Method3.6 Volumes of Revolution: The Shell Method3.7 Calculating the Length of a Curve3.8 Calculating the (Lateral) Area of a Surface3.9 Parting ThoughtsChapter 3 AppendixA3.1 Area between Two Curves: The Riemann Sums ApproachA3.2 Riemann Sums Approach to Volumes by Cross SectionsA3.3 Riemann Sums Approach to the Disk MethodA3.4 Riemann Sums Approach to the Washer MethodA3.5 Riemann Sums Approach to the Shell MethodA3.6 Volumes of Revolution: Noncoordinate Axes of Revolution
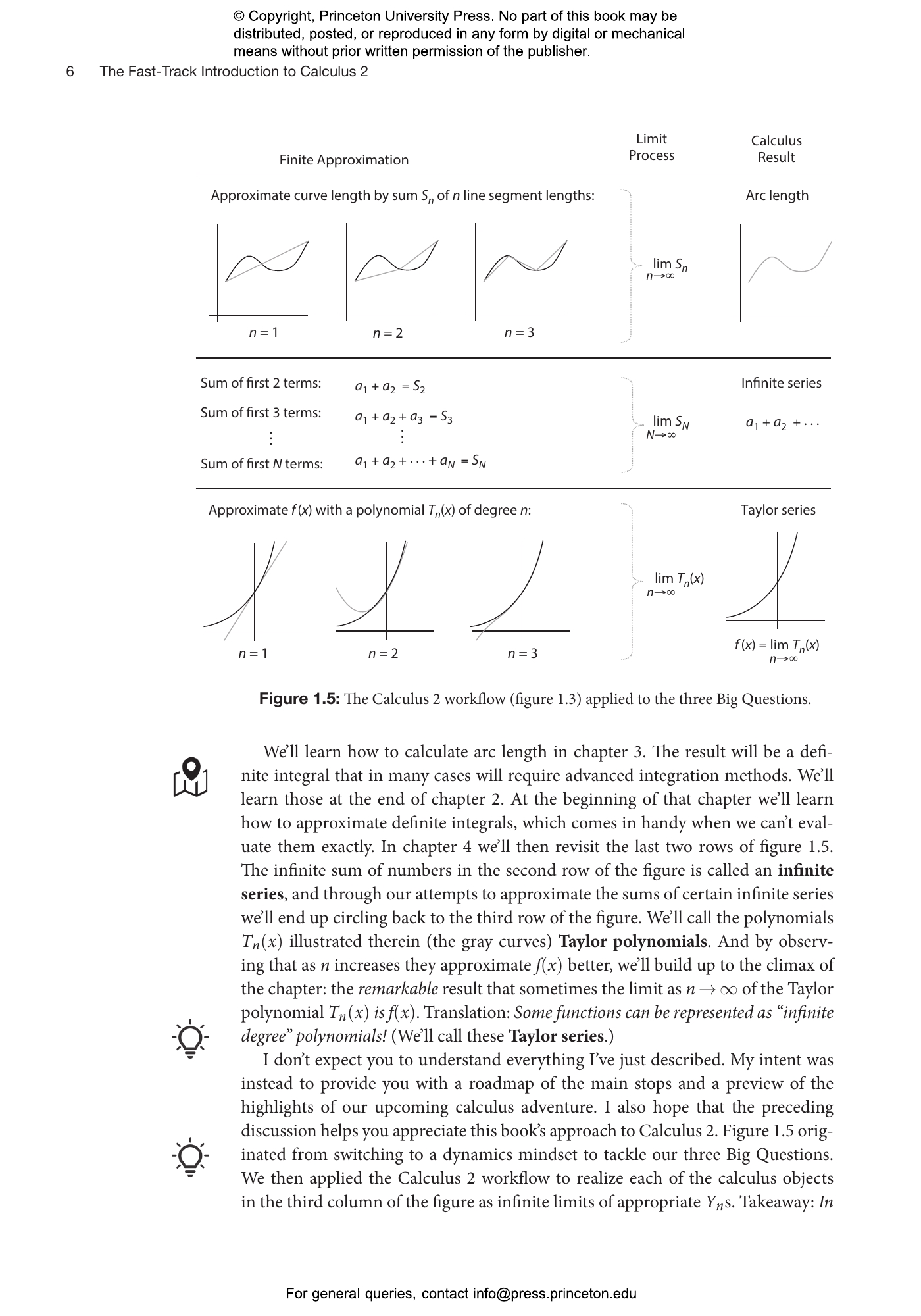
4.1 Introduction to Sequences4.2 Convergence of Sequences4.3 Inï¬nite Series4.4 Special Series and the Series Laws4.5 The Limit and Direct Comparison Tests4.6 Alternating Series4.7 The Ratio Test4.8 Approximating the Sum of an Alternating Series4.9 Taylor Polynomials4.10 Taylorâs Theorem4.11 Power Series and Their Convergence4.12 Power Series as Functions4.13 Taylor Series4.14 Convergence of Taylor Series4.15 Applications of Taylor Series4.16 Parting Thoughts
- 5 Connections between Integration and Series
5.1 Partial Fractions and Telescoping Series5.2 Power/Taylor Series and Integration5.3 Improper Integrals5.4 The Integral Test for Series5.5 Parting Thoughts
- Appendixes A—D: Precalculus and Calculus Review
A Algebra and Geometry ReviewB Precalculus (Functions) ReviewC Calculus Review IâThrough Diï¬erentiationD Calculus Review IIâIntegration
- Appendix E: Integration Basics
E.1 The Fundamental Theorem of CalculusE.2 Antiderivatives and the Evaluation TheoremE.3 Properties of IntegralsE.4Net Signed AreaE.5 Integrating Transcendental FunctionsE.6 The Substitution Rule
- Appendix F: LâHôpitalâs Rule
- Answers to Exercises
- Bibliography
- Index of Applications
- Subject Index
“Keeping the reader in mind, Fernandez strikes a balance between the competing demands for a Calculus 2 class.”—Shahriar Shahriari, author of An Invitation to Combinatorics and Approximately Calculus
“Fernandez does a great job of meeting the students where they are and taking them further on the calculus pathway. Calculus 2 Simplified is inviting and easy to read, with well-chosen examples and engaging problems that will challenge students and hold their attention.”—David Dorman, Middlebury College
“This book is a uniquely effective tool for students to learn calculus. It offers bite-size treatments of topics, maintaining the formality of the mathematics while developing intuition and understanding, and includes a plethora of exercises that gives students a large set of problems to practice with.”—Marcel Blais, Worcester Polytechnic Institute